Apr. 3, 2017
観測点の位置を,3点の既知点を視準して,算出するVisual Basic Macro on MS Excelをここに掲載する。測量や入力手順を次にしめす。
0.
原理は,たとえば次のpdfに示されている。
http://www.infra.kochi-tech.ac.jp/takagi/Survey1/8Backward.pdf
1. 水平角を求め得る望遠鏡つきの機器が必要である。
2. Google Earthで観察が可能なランドマークをさがす。タワー,道路の交差点,比較的大きな建物の隅。ここでの例は,道路と河川の交差点,赤い屋根の端,電波塔である。
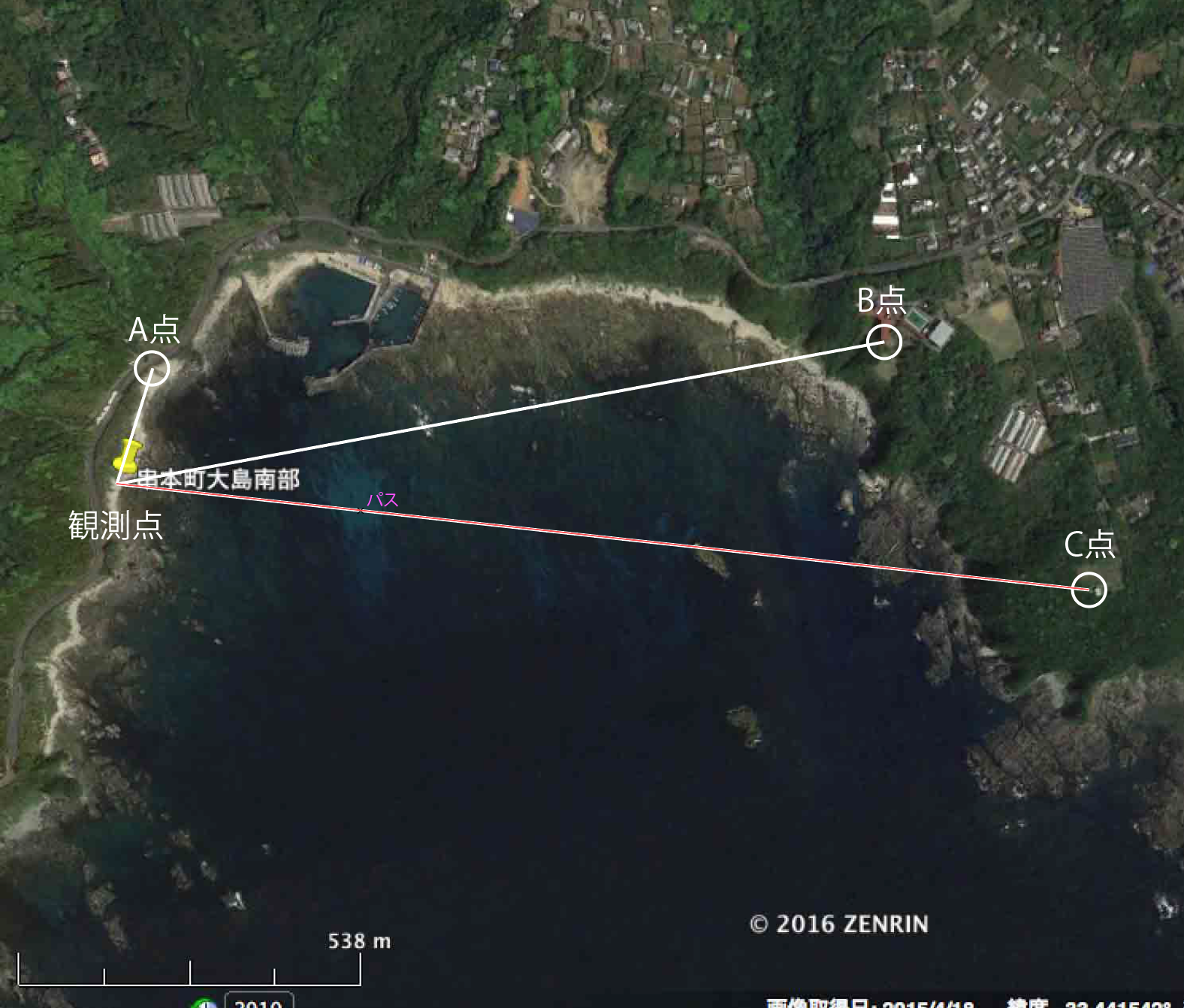
3. ランドマークは向かって左手から右手,つまり時計回りに視準する。A点,B点,C点の3方向の視準をすると2夾角ができるが,誤差を最小限に止めるには90度プラマイ40度としたいが,これが結構難しい。次の図にその様子を示す。VBでの変数は,M(1,0),M(2,0), M(3,0)。夾角は,K(1)とK(2)にあたる。

4. フィールドでは,A, B, Cへの3本の視準角度(度分秒)を得ることになる。もちろん,視準先の写真は撮影した方がいいだろう。iPhoneなどであればGPSで撮影地点の経緯度などを取得できるので,求める精度によっては,この作業そのものが不要ではある。
5. フィールドから戻って,Google Earthで3点A, B, Cの経緯度を求め,国土地理院のサイトで平面直角座標系の座標値(northing X, easting Y)を変換する必要がある。
6. エクセルのマクロを使って計算するのであるがその入力と出力画面のスクリーンショットを次に示す。

7. 計算 エクセルファイルのダウンロード
上のエクセル画面の,クリーム色のセルは,入力スペースである。利用者はここに入力してほしい。spreadsheetはマクロでは,sheet1,にしているので,適宜変更していただければいい。
マクロの実行は所定の手続きを経て実行する。その出力は水色のセルに表示される。
グラフィック表示は手作業で実施してほしい。与点3点と観測点の座標値を,下の,散布図データ,の欄に,テキストペーストしてほしい。その結果,既存のグラフが生かされるが,値によっては表示が適切ではないので,縦と横がほぼ同じになるように縦横の比率を変えるなど,各自が触ってね。
なお,このマクロを作成する上で,
岸塚正昭,1986.後方交会法計算アルゴリズムとその造園工事出来形測量への試用.造園雑誌, Vol. 50, No. 5, pp. 143-148.
を参考にさせていただいた。感謝いたします。今日はぼくの誕生日(68歳だって)。
8. ご参考:
Apr02_2017_3completed
Sub BackwardIntersection()
' *****Naming three given points as A, B, C clockwise from an instrument
' *****Composed at Mar. 31, 2017
Dim I As Integer, J As Integer: Dim SA As Double, SC As Double
Dim X As Double, Y As Double
Dim M(3, 6) As Double, K(2) As Double
Pi = 3.14159265359
' *****Inputting of northig-X values of three given points
For I = 1 To 3
M(I, 1) = Worksheets("Sheet1").Cells(10 + I, 2)
Next I
' *****Inputting of easting-Y values of three given points
For I = 1 To 3
M(I, 2) = Worksheets("Sheet1").Cells(10 + I, 3)
Next I
' *****Calculation of sides and angles of a triangular ABC
For I = 1 To 3
J = I + 1: If J = 4 Then J = 1
X = M(J, 1) - M(I, 1): Y = M(J, 2) - M(I, 2)
M(I, 3) = Sqr(X ^ 2# + Y ^ 2#): ' *****c, a, b sides
X = X / M(I, 3): M(I, 4) = 0.5 * Pi - Atn(X / Sqr(-X * X + 1#)): ' ***AB BC CA azimuths
If Y < 0 Then M(I, 4) = 2# * Pi - M(I, 4)
Next I
' *****Calculation of intersection angles of a triangular ABC
For I = 1 To 3: J = I - 1: If J = 0 Then J = 3
M(I, 5) = M(J, 4) - M(I, 4) + Pi: ' *****intersection angles
If M(I, 5) > 2# * Pi Then M(I, 5) = M(I, 5) - 2# * Pi
If M(I, 5) < -2# * Pi Then M(I, 5) = M(I, 5) + 2# * Pi
Next I
M(0, 5) = 0
For I = 1 To 3
M(0, 5) = M(0, 5) + M(I, 5) * 180# / Pi
Next I
' *****Inputting of horizontal angles (rad) of collimation axes to A, B, C
For I = 1 To 3
M(I, 0) = (Worksheets("Sheet1").Cells(10 + I, 8)) / 180 * Pi
Next I
' *****Calculation of circumcenters of angles APB and BPC
For I = 1 To 2
K(I) = M(I + 1, 0) - M(I, 0)
Next I
M(0, 0) = 2# * Pi - K(1) - K(2) - M(2, 5)
SA = M(2, 3) * Sin(K(1))
SC = M(1, 3) * Sin(K(2))
M(0, 6) = Atn(SA * Sin(M(0, 0)) / (SA * Cos(M(0, 0)) + SC))
If M(0, 6) < 0 Then M(0, 6) = M(0, 6) + Pi
M(3, 6) = M(0, 0) - M(0, 6)
M(1, 6) = Pi - M(0, 6) - K(1)
M(2, 6) = M(2, 5) - M(1, 6)
If M(2, 6) < 0 Then M(2, 6) = M(2, 6) + 2 * Pi
If K(1) = 0 Then GoTo label01 Else M(0, 4) = M(1, 4) + M(0, 6)
M(0, 3) = M(1, 3) * Sin(M(1, 6)) / Sin(K(1)): I = 1: GoTo label02
label01: M(0, 4) = M(3, 4) + M(3, 5) - M(3, 6)
M(0, 3) = M(2, 3) * Sin(M(2, 6)) / Sin(K(2)): I = 3
' *****Calculation and output of northing and easting values of the instrument obtained
label02: M(0, 1) = M(0, 3) * Cos(M(0, 4)) + M(I, 1)
M(0, 2) = M(0, 3) * Sin(M(0, 4)) + M(I, 2)
For I = 1 To 2
Worksheets("Sheet1").Cells(16, I + 1) = M(0, I)
Next I
End Sub
以 上