2006-11-25作成 Jan.2,'08追加 Dec. 2, 09追加 Oct. 13, 15修正
もくじ
測点の地磁気補正
測点の測地系への位置づけ
測地系変換のためのUTM図法の基礎
UTM ←→ 経緯度変換
平面直角座標系の距離値から経緯度を計算
現地調査や測量では,複数の既存の基準点を利用するのがいいが,研究のための測量はそれほどの位置精度を必要としない。数キロメートル離れた2地点から現場の仮基準点の座標値を求める労力は大きいし,次に述べる方法よりも位置精度が下がる可能性がある。そこで,真北を求めるのに磁北を使い,地図上の
位置を求めるのに携帯用のGPSを使うことになる。
磁北から真北をWeb上で求めるプログラムが公開されている:経緯度から地磁気を求めるプログラム (国土地理院の「地磁気値を求める」)
緯度・経度とも,秒までの精度である(ITRF座標系GRS80楕円体の位置座標,つまり世界測地系=日本測地系2000)。たとえば与論島百合の浜の27゜02′11″N,128゜27′08″Eでは,
全磁力 44473 nT(Teslaは10,000 gauss アメリカの電磁気誘導の研究者ニコラ・テスラの名前から),偏角4゜26′(西偏),伏角38゜51′。
用語については,国土地理院地磁気測量に掲載されている。
測量範囲が連続した領域であれば,わざわざ世界測地系に載せる必要性はないのだが,不連続であれば,測地系に載せるのが適当である。
経緯度からUTM座標系またはその逆の変換法は後述する。なお,通常の研究での測量結果はUTMよりも平面直角座標系に落とすのが精度も高く利用上の便宜もいい。
国土地理院には,Web上で求める次のプログラムなどが公開されている:
緯度・経度と地心直交座標の相互換算ーー 緯度、経度、標高、ジオイド高と地心直交座標(X,Y,Z値)との相互換算を行う
距離と方位角の計算ーー緯度、経度から2点間の距離と方位角を求める
距離と方向角の計算ーーXY座標から2点間の距離と方向角を求める
平面直角座標への換算ーー緯度、経度から平面直角座標へ換算する
緯度、経度への換算ーー平面直角座標から緯度、経度へ換算する
世界測地系座標変換(TKY2JGD) ーー日本測地系に基づく経緯度および平面直角座標を 世界測地系に基づく経緯度および平面直角座標への変換
ジオイド高計算ーー日本のジオイド 2011モデルを使用
なお,回転楕円体,ジオイド高,標高の関係は次のサイトに。
各種座標系間変換プログラムは飛田幹男氏によって公開されている(飛田幹男,2002. 世界測地系と座標変換 ー 21世紀の測量士・位置情報ユーザープログラマーのために. 日本測量協会,174p, 1600円)。Windows 95/98対応のプログラムは,他のソフトとともに,日本測量協会の本部(東京)でのみ販売されている。CDロム付き ー 12,000円(送料別途 650円)。内容については次のサイトに掲載されている。
世界測地系対応ソフトウェア集 「世界測地系と座標変換」関連ソフトウェア。
UTMと経緯度との間の変換をする上で,UTM図法の基礎知識が必要となる。
変換をする上でその場所が北半球か南半球か,西経の領域か東経の領域かを知る必要がある。N or S, W or Eを外すと同じ数値の経緯度が地球には4点ある。UTMの[Northing (x), Easting (y)]の座標値については同じものが 120点もある。
UTM座標系の全体像は次のようである。つぎの図を参照して欲しい:
http://www.dmap.org.uk/utmworld.gif
この注記によると,太平洋のほぼ中央にある西経180度線を出発して,東回りに一周するまでに経度6度のゾーンが60個できる。zone1は,180度W-174度Wである。最後のzone60は,174E-180Eである。180Wと180Eは一致している。沖縄県はzones 51,52,近畿地方はzone53にあたる。北海道東端はzone55である。
図にあるように80度S-84度Nの間の緯線ゾーンが20区分されている。アルファベットのCからXまでが南から北に使用されており,途中,I,Oが使われていないので,緯度8度ずつ(Xだけ12度)で20区分になる。UTM座標のそれぞれの位置はこの経緯度ゾーンのいずれかに入る。たとえば,近畿地方は53Sになる。GPS器を大阪の自宅で使うと,UTM 53 S 0545192 3855438と表示される。Zone 53Sで,(y,x) =(Easting, Northing)= (0545192m, 3855438m)を意味する。
zone 53の中央経線は日本標準時子午線にあたる。GPSで使用されている測地系はアメリカの定めたWGS84座標系である。2002年4月より導入された世界測地系の東経135度子午線は、日本測地系の子午線より約260m東側を通っている。これは国際地球回転事業で定めたITRF座標系が使用されているが,2万5千分のⅠ地図上で1mmほどしか違いが無いので通常の利用では問題がない。
UTMの経度ゾーンの原点は,(Easting, Northing)= (500000,0)とされている。それゆえ,ぼくの自宅は,東経135度線と赤道が交わる原点からすると,東に545,192 - 500,000 =45,192m, 北に 3,855,438m 離れていることになる。
経緯度からUTMへの変換は,次のサイトでエクセルのワークシートに入力することで換算できる。
Transverse Mercator Calculator http://www.dmap.co.uk/ll2tm.htm で可能である。ただ,このサイトでは双方向の変換についてはExcelのワークシート£15が必要となる。
次のサイトでは無料のエクセルシートが公開されており(GISContents/GIS_dwnld/UTMConversions1.xls),自分のワークシートに組み込んでもいいとのこと(Steven Dutch, Natural and Applied Sciences, University of Wisconsin - Green Bay)。使用法は次のサイトにある。How to Use the Spreadsheet for Converting UTM to Latitude and Longitude (Or Vice Versa) http://www.uwgb.edu/dutchs/UsefulData/HowUseExcel.HTM
日本の測地座標系の説明 http://vldb.gsi.go.jp/sokuchi/datum/tokyodatum.html
座標系は、地点の座標値が次の条件に従ってガウスの等角投影法によって表示されるように設けるものとする。
1 .座標系のX軸は、座標系原点において子午線に一致する軸とし、真北に向う値を正とし、座標系のY軸は、座標系原点において座標系のX軸に直交する軸とし、真東に向う値を正とする。
2 .座標系のX軸上における縮尺係数(本ページの最下部で説明する)は、0.9999とする。 3 .座標系原点の座標値は、次のとおりとする。 X=0.000メートル Y=0.000メートル 日本の平面直角座標系(公共座標系、19座標系)
http://vldb.gsi.go.jp/sokuchi/patchjgd/download/Help/jpc/jpc.htm
大阪の系番号は6。この座標系原点は福井県南部136度 0分0秒 36度0分0秒にある。6系の主な カバー範囲は, 京都府 大阪府 福井県 滋賀県 三重県 奈良県 和歌山県。
例えば,大阪府 1:3000地形図 大K5-8(昭和36年測量)を見ると,左上隅(ほぼ方眼南北線,ほぼ方眼東西線)= (-126,-42),右下隅(ほぼ方眼南北線,ほぼ方眼東西線)= (-128,-39)。この(x, y)関係は誤解しやすい。ぼくも当初誤解した。-42と-39の数字は図廓の地図が読めるように開いている場合,右に90度回転した時に読める表記になっている。つまり,原点から西方向への距離-42000m,-39000mを表している。つまり,y軸方向を表す。-126と-128は,そのまま読める,つまり南方向への距離-126000,-128000mを表している。つまり,x軸方向を示している。(x(方眼南北線), y(方眼東西線))の配列になっている訳である。
この図幅の下部には,「座標系は国土調査法施工令(昭和27年政令第59号)第2条の規定による第VI座標系投影はガウスの等角投影法図法,図廓に表示してある座標値はキロメートル単位,高さの基準は東京湾中等潮位(T.P)O.P+1.046m,等高線の間隔は2メートル」 平面直角座標系6。
さて,実際の変換サイトは, http://www.n-survey.com/online/xybl.htm である。これは国土地理院のサイトのコンテンツを生かしながら,Google Mapに変換点が表示される。実際の地図で確認できるのである。
ここで,
世界測地系,平面直角座標,そして,第6系とする。 緯度・経度の形式は「ddmmss.sssss」とある。
(x, y)= (-126000, -42000)を入力した際の表示を次に示す。入力データ,出力データが下部のウィンドに表示される。csv形式(comma separated value)がいいだろう。
http://www.n-survey.com/online/gmap.htm
AISAN Technology Co., Ltd.のサイトが参考になる。改変して転載する。

上の図は楕円体面の座標P(φ(ふぁい,緯度),λ(らむだ,経度))と平面直角座標系のP'(x, y)の対応関係を示している。
縮尺係数 m は,
楕円体面の微小距離 dS とそれに対応する平面直角座標系の微小距離 ds の比
m=(ds/dS)
で表される。等角条件を満たすためには、この m は全方向とも等しい「等方向性(isotropy)」でなくてはならない。m として作業規程の準則には、「成果表に記載する縮尺係数」として、次式が使われている。
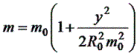 式
式
ただし、R0 :座標原点での平均曲率半径、m0 :中央子午線での縮尺係数(0.9999)
この式でわかるように,縮尺係数はy座標値だけできまる。下の図のように,原点から離れるにつれて,縮尺係数の変化が大きくなる。
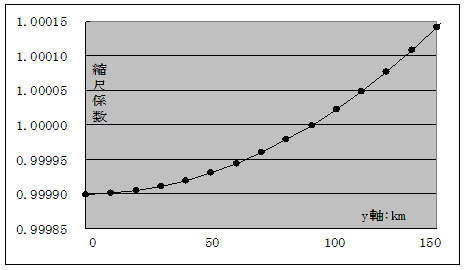
さて,地図センターの図を次に示す。
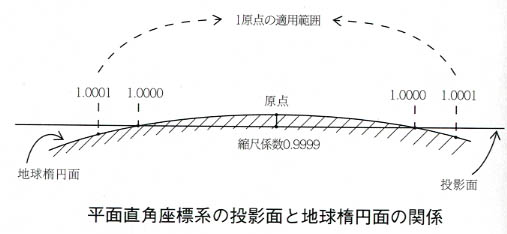
この図中央の原点の部分に中央子午線が走る。左右の弧状線は地球楕円体面,水平線は平面直角座標系の投影面。投影面の適用範囲は縮尺係数で1.0001まで。
以 上